有一個程式設計師住在一條街上,這條街上的房子都在路的同一邊且門牌號碼是從1-2-3-4-....連續下來。有一天晚上他牽著他的狗出門散步,出門之後往左邊走,因為溜狗有點無聊,所以她順便把經過的房子的門牌號碼都加起來。隔天晚上他又出門溜狗,但這一次她往右走並且也把經過的門牌號碼加起來。讓他很驚訝的是:這兩次的數字竟然一樣。
當然,這個巧合現象跟這條街共有幾間房子(n),以及他住在第幾間房子(k)有關係。請寫出一個程式找出前十個滿足這樣條件的數對(k,n)。在輸出中有前2個這樣的數對。
每一對數字k,n的長度均為10,向右靠齊。請將檔案輸出至"out.txt"。 ※此題無須"in.txt"
輸出範例:
6 8
35 49
出自 程式設計隊訓練教材 NO.34 門牌號碼
參照 http://chscvb.blogspot.com/2010/01/20100125.html
2010年12月20日 星期一
2010年11月8日 星期一
Problem 5(8%):傳統數學問題的解決(99模擬)
子題1:給定若干個數字,將它們依序排成一個頭、尾相接的環形。如果我們從某一數字開
始點名,每次點名後再往後跳2 個數字繼續點名(中間間隔1 個未被點名的數字)。已經被點
到名的數字不可再點,直到剩下最後一個「未點名」的數字時才停止。請問最後的數字為何?
輸入說明:
第1 行依序給定最多20 個要點名的數字,各數字之間以逗號隔開。
第2 行有1 個數字,是「開始點名」的數字。
輸出說明:
第1 行輸出最後一個未點名的數字。
輸入範例:【檔名:in-5-1.txt】
5, 3, 7, 11, 4, 2, 1, 8, 9
8
輸出範例:【檔名:out-5-1.txt】
9
子題2(8%):如果有一個正整數n,其值等於所有n 的因數(除了n 以外)之總合,則n 稱
為「完美數」(Perfect number)。在此計算中,其「因數」不限制為「質因數」。請輸出2 到數
字k 之間的完美數。
輸入說明:
第1 行有1 個數字,代表k 的值。而k 的值不超過50000。
輸出說明:
每行輸出1 個範圍內的完美數,依其值由小到大輸出。
輸入範例:【檔名:in-5-2.txt】
10000
輸出範例:【檔名:out-5-2.txt】
6
28
496
8128
始點名,每次點名後再往後跳2 個數字繼續點名(中間間隔1 個未被點名的數字)。已經被點
到名的數字不可再點,直到剩下最後一個「未點名」的數字時才停止。請問最後的數字為何?
輸入說明:
第1 行依序給定最多20 個要點名的數字,各數字之間以逗號隔開。
第2 行有1 個數字,是「開始點名」的數字。
輸出說明:
第1 行輸出最後一個未點名的數字。
輸入範例:【檔名:in-5-1.txt】
5, 3, 7, 11, 4, 2, 1, 8, 9
8
輸出範例:【檔名:out-5-1.txt】
9
子題2(8%):如果有一個正整數n,其值等於所有n 的因數(除了n 以外)之總合,則n 稱
為「完美數」(Perfect number)。在此計算中,其「因數」不限制為「質因數」。請輸出2 到數
字k 之間的完美數。
輸入說明:
第1 行有1 個數字,代表k 的值。而k 的值不超過50000。
輸出說明:
每行輸出1 個範圍內的完美數,依其值由小到大輸出。
輸入範例:【檔名:in-5-2.txt】
10000
輸出範例:【檔名:out-5-2.txt】
6
28
496
8128
Problem 4:排列組合的應用(99模擬)
子題1(11%):一個菜販有「肉」、「菜」、「蛋」、「果」4 類商品,在菜攤上「分類」排列出
售,各項商品可由輸入檔讀入其「每公斤利潤」。有一天,菜販忘了商品在菜攤的排列方式,
只知道今天各類商品由左至右出售的「公斤數」,其資料選手也可由輸入檔讀入。在不知道今
天商品排列的情況下,請選手將所有的排列方式逐一代入計算,依總利潤之高低順序,由高
而低,輸出所有排列方式及其總利潤。
輸入說明:
第1 行有4 組數字,以逗號隔開,分別表示「肉」、「菜」、「蛋」、「果」每公斤的利潤。
第2 行有4 組數字,以逗號隔開,表示今天菜攤由左至右各類商品出售之公斤數。
輸出說明:
依總利潤之高低順序,每1 行輸出1 組排列方式及其總利潤,資料間至少以1 個空白隔開。
若有總利潤相同者,其前後輸出順序不拘。
輸入範例:【檔名:in-4-1.txt】
70, 32, 18, 42
43, 24, 21, 39
輸出範例:【檔名:out-4-1.txt】
肉菜蛋果 5794
肉蛋菜果 5752
果菜蛋肉 5682
肉果蛋菜 5644
果蛋菜肉 5640
肉蛋果菜 5572
菜果蛋肉 5492
菜蛋果肉 5420
肉果菜蛋 5392
肉菜果蛋 5362
蛋果菜肉 5184
蛋菜果肉 5154
果肉蛋菜 5112
菜肉蛋果 5072
果蛋肉菜 4956
菜蛋肉果 4916
果肉菜蛋 4860
蛋肉菜果 4764
果菜肉蛋 4746
蛋菜肉果 4650
菜肉果蛋 4640
蛋肉果菜 4584
菜果肉蛋 4556
蛋果肉菜 4500
子題2(11%):如果有一個客人來買這個菜攤的n 項商品,每類商品只能買1 項或不買,請
選手列出所有可能的購買組合。輸出之順序,應依照購買之總金額由高而低依序輸出。
輸入說明:
第1 行有1 個數字,代表n 的值。
第2 行有4 組數字,以逗號隔開,分別表示「肉」、「菜」、「蛋」、「果」每項商品的購買金額。
輸出說明:
每列輸出一組購買組合及其購買總金額,並至少以1 個空白隔開。其輸出方式為:每列均輸
出「肉菜蛋果」字串,但客人「購買」之商品名稱以「小括號」括起來。輸出之順序依購買
之總金額由高而低依序輸出,若有總金額相同者則不限順序。
輸入範例:【檔名:in-4-2.txt】
2
140, 64, 36, 84
輸出範例:【檔名:out-4-2.txt】
(肉)菜蛋(果) 224
(肉)(菜)蛋果 204
(肉)菜(蛋)果 176
肉(菜)蛋(果) 148
肉菜(蛋)(果) 120
肉(菜)(蛋)果 100
售,各項商品可由輸入檔讀入其「每公斤利潤」。有一天,菜販忘了商品在菜攤的排列方式,
只知道今天各類商品由左至右出售的「公斤數」,其資料選手也可由輸入檔讀入。在不知道今
天商品排列的情況下,請選手將所有的排列方式逐一代入計算,依總利潤之高低順序,由高
而低,輸出所有排列方式及其總利潤。
輸入說明:
第1 行有4 組數字,以逗號隔開,分別表示「肉」、「菜」、「蛋」、「果」每公斤的利潤。
第2 行有4 組數字,以逗號隔開,表示今天菜攤由左至右各類商品出售之公斤數。
輸出說明:
依總利潤之高低順序,每1 行輸出1 組排列方式及其總利潤,資料間至少以1 個空白隔開。
若有總利潤相同者,其前後輸出順序不拘。
輸入範例:【檔名:in-4-1.txt】
70, 32, 18, 42
43, 24, 21, 39
輸出範例:【檔名:out-4-1.txt】
肉菜蛋果 5794
肉蛋菜果 5752
果菜蛋肉 5682
肉果蛋菜 5644
果蛋菜肉 5640
肉蛋果菜 5572
菜果蛋肉 5492
菜蛋果肉 5420
肉果菜蛋 5392
肉菜果蛋 5362
蛋果菜肉 5184
蛋菜果肉 5154
果肉蛋菜 5112
菜肉蛋果 5072
果蛋肉菜 4956
菜蛋肉果 4916
果肉菜蛋 4860
蛋肉菜果 4764
果菜肉蛋 4746
蛋菜肉果 4650
菜肉果蛋 4640
蛋肉果菜 4584
菜果肉蛋 4556
蛋果肉菜 4500
子題2(11%):如果有一個客人來買這個菜攤的n 項商品,每類商品只能買1 項或不買,請
選手列出所有可能的購買組合。輸出之順序,應依照購買之總金額由高而低依序輸出。
輸入說明:
第1 行有1 個數字,代表n 的值。
第2 行有4 組數字,以逗號隔開,分別表示「肉」、「菜」、「蛋」、「果」每項商品的購買金額。
輸出說明:
每列輸出一組購買組合及其購買總金額,並至少以1 個空白隔開。其輸出方式為:每列均輸
出「肉菜蛋果」字串,但客人「購買」之商品名稱以「小括號」括起來。輸出之順序依購買
之總金額由高而低依序輸出,若有總金額相同者則不限順序。
輸入範例:【檔名:in-4-2.txt】
2
140, 64, 36, 84
輸出範例:【檔名:out-4-2.txt】
(肉)菜蛋(果) 224
(肉)(菜)蛋果 204
(肉)菜(蛋)果 176
肉(菜)蛋(果) 148
肉菜(蛋)(果) 120
肉(菜)(蛋)果 100
Problem 3:子字串特徵的判斷(99模擬)
此問題為給定某些英文文句,其內容只有「英文、數字、空白及標點符號」,請選手判斷此文
句是否符合某些檢查條件?
子題1(10%):是否文句中存在任何子字串,其以「任一數字」開頭,「任一數字」結尾,中
間存在1 個至3 個大寫字母。
輸入說明:
第1~3 行表示欲檢查之3 句英文文句。
輸出說明:
第1~3 行分別對應第1~3 句檢查文句,若存在符合條件之子字串即輸出「有」,不存在即輸出
「沒有」。
輸入範例:【檔名:in-3-1.txt】
Tom Lin’s employee number is A123BSC45.
The price is 45 US dollars.
The machine code is 65K2.
輸出範例:【檔名:out-3-1.txt】
有
沒有
有
子題2(10%):是否文句中存在任何子字串,其為「合理」的「台北市」、「台中市」或「高
雄市」身份證字號。
註:
(1) 身份證字號第1 碼為地區碼,「台北市」以「A」開頭、「台中市」以「B」開頭、「高雄市」
以「E」開頭。
(2) 身份證字號的第2 碼為「性別」碼,其值應為「1」或「2」。
(3) 若將身份證字號的「地區碼」改為2 碼數字,其中「A」改為「10」、「B」改為「11」、「E」
改為「14」,其後併入原身份證後9 碼數字,成為1 個新的11 位數字碼。將此數字碼由左
至右分別乘以「1、9、8、7、6、5、4、3、2、1、1」,其相乘後的總和應可被10 整除。
輸入說明:
第1~3 行表示欲檢查之文句。
輸出說明:
若存在合理的身份證字號即輸出「有」,不存在即輸出「沒有」。
輸入範例:【檔名:in-3-2.txt】
His ID number is A120441768.
Her ID number is B272857734.
Their ID numbers are E286585485, E282467997, and E195445887.
輸出範例:【檔名:out-3-2.txt】
有
沒有
有
句是否符合某些檢查條件?
子題1(10%):是否文句中存在任何子字串,其以「任一數字」開頭,「任一數字」結尾,中
間存在1 個至3 個大寫字母。
輸入說明:
第1~3 行表示欲檢查之3 句英文文句。
輸出說明:
第1~3 行分別對應第1~3 句檢查文句,若存在符合條件之子字串即輸出「有」,不存在即輸出
「沒有」。
輸入範例:【檔名:in-3-1.txt】
Tom Lin’s employee number is A123BSC45.
The price is 45 US dollars.
The machine code is 65K2.
輸出範例:【檔名:out-3-1.txt】
有
沒有
有
子題2(10%):是否文句中存在任何子字串,其為「合理」的「台北市」、「台中市」或「高
雄市」身份證字號。
註:
(1) 身份證字號第1 碼為地區碼,「台北市」以「A」開頭、「台中市」以「B」開頭、「高雄市」
以「E」開頭。
(2) 身份證字號的第2 碼為「性別」碼,其值應為「1」或「2」。
(3) 若將身份證字號的「地區碼」改為2 碼數字,其中「A」改為「10」、「B」改為「11」、「E」
改為「14」,其後併入原身份證後9 碼數字,成為1 個新的11 位數字碼。將此數字碼由左
至右分別乘以「1、9、8、7、6、5、4、3、2、1、1」,其相乘後的總和應可被10 整除。
輸入說明:
第1~3 行表示欲檢查之文句。
輸出說明:
若存在合理的身份證字號即輸出「有」,不存在即輸出「沒有」。
輸入範例:【檔名:in-3-2.txt】
His ID number is A120441768.
Her ID number is B272857734.
Their ID numbers are E286585485, E282467997, and E195445887.
輸出範例:【檔名:out-3-2.txt】
有
沒有
有
Problem 2:資料表示方式的應用(99模擬)
子題1(12%):在一張地圖上標示有若干個城市,及一些可雙向通行的道路。這些道路的頭、
尾,各連接一個不同的城市。我們用1 個一維整數陣列(假設稱為a 陣列),存放各個城市連
接的道路數目(存放順序不限)。為了判斷陣列中存放的道路數目值,是否可以正確的表達某
一張地圖上城市及道路的關係,我們利用以下步驟檢查(假設陣列的指標由1 開始):
步驟1:我們將陣列由大到小排序,令排序後的陣列為b 陣列。
步驟2:假設b(1) = k,我們將b(2)到b(k +1)共k 個元素,每個元素值都減1。
步驟3:我們將b(1)從b 陣列中移除,得一個「新陣列」。
第 3 頁,共 8 頁
步驟4:如果「新陣列」中,存在任何一個小於0 的元素值,原始a 陣列就是「不正確」陣列;
如果「新陣列」中的所有元素均等於0,原始a 陣列就是「正確」陣列。若在此步驟
達成判斷,檢查即可結束。
步驟5:在不能判斷正確與否時,將「新陣列」代入步驟1,重覆上述檢查,直到達成判斷條
件為止。
輸入說明:
第1~4 行表示將判斷之4 組陣列值,各元素間以逗號區隔,每組陣列最多有10 個元素。輸入
檔之元素值,不會造成選手進行「步驟2」時產生「陣列索引值超出範圍」的錯誤。
輸出說明:
第1~4 行分別輸出第1~4 組陣列的正確與否。當正確輸出「正確」,不正確時輸出「不正確」。
輸入範例:【檔名:in-2-1.txt】
1, 1, 2, 5, 3, 2
4, 3, 1, 1, 1
4, 4, 4, 3, 3
3, 3, 3, 3, 3
輸出範例:【檔名:out-2-1.txt】
正確
不正確
正確
不正確
子題2(12%):在圖形結構中,有一種特別的圖形,稱之為「樹狀圖」(Tree)。在一個樹狀
圖中,包含若干個「節點」,每個節點和它的「上一層節點」及「下一層節點」相連。每個節
點有「1 個」或是「沒有」上一層節點;也可能有「1 個」、「多個」或是「沒有」下一層節點。
這些節點中,只有1 個節點沒有上一層節點,所以它是最頂層的節點,我們稱之為「樹根」;
其他「非樹根」的節點,都有1 個上一層節點,我們稱這些「上一層節點」是該節點的「父
親」。現在給定一個樹狀圖資料,並給一個「目的地」節點名稱,請選手輸出從「樹根」連接
到目的地經過的所有節點。輸出資料的順序,應從「樹根」開始,一層一層向下,最後到達
「目的地」節點依序輸出,輸出的節點不能重覆。
輸入說明:第1 行表示共有多少個節點;第2 行是目的地節點;第3 行起是所有節點資料,
每行有一組符號以逗號隔開,第1 個符號為「節點名稱」,第2 個符號為其「父親名稱」。若
是「樹根」節點,其父親表示為「---」3 個連續減號。
輸出說明:列出從「樹根」連接到目的地經過的所有節點(包括樹根與目的地節點),而輸出
的節點間至少以1 個空白相隔開。
輸入範例:【檔名:in-2-2.txt】
11
K
A, ---
B, A
C, A
D, B
E, B
F, C
G, E
H, G
I, G
J, I
K, I
輸出範例:【檔名:out-2-2.txt】
A B E G I K
尾,各連接一個不同的城市。我們用1 個一維整數陣列(假設稱為a 陣列),存放各個城市連
接的道路數目(存放順序不限)。為了判斷陣列中存放的道路數目值,是否可以正確的表達某
一張地圖上城市及道路的關係,我們利用以下步驟檢查(假設陣列的指標由1 開始):
步驟1:我們將陣列由大到小排序,令排序後的陣列為b 陣列。
步驟2:假設b(1) = k,我們將b(2)到b(k +1)共k 個元素,每個元素值都減1。
步驟3:我們將b(1)從b 陣列中移除,得一個「新陣列」。
第 3 頁,共 8 頁
步驟4:如果「新陣列」中,存在任何一個小於0 的元素值,原始a 陣列就是「不正確」陣列;
如果「新陣列」中的所有元素均等於0,原始a 陣列就是「正確」陣列。若在此步驟
達成判斷,檢查即可結束。
步驟5:在不能判斷正確與否時,將「新陣列」代入步驟1,重覆上述檢查,直到達成判斷條
件為止。
輸入說明:
第1~4 行表示將判斷之4 組陣列值,各元素間以逗號區隔,每組陣列最多有10 個元素。輸入
檔之元素值,不會造成選手進行「步驟2」時產生「陣列索引值超出範圍」的錯誤。
輸出說明:
第1~4 行分別輸出第1~4 組陣列的正確與否。當正確輸出「正確」,不正確時輸出「不正確」。
輸入範例:【檔名:in-2-1.txt】
1, 1, 2, 5, 3, 2
4, 3, 1, 1, 1
4, 4, 4, 3, 3
3, 3, 3, 3, 3
輸出範例:【檔名:out-2-1.txt】
正確
不正確
正確
不正確
子題2(12%):在圖形結構中,有一種特別的圖形,稱之為「樹狀圖」(Tree)。在一個樹狀
圖中,包含若干個「節點」,每個節點和它的「上一層節點」及「下一層節點」相連。每個節
點有「1 個」或是「沒有」上一層節點;也可能有「1 個」、「多個」或是「沒有」下一層節點。
這些節點中,只有1 個節點沒有上一層節點,所以它是最頂層的節點,我們稱之為「樹根」;
其他「非樹根」的節點,都有1 個上一層節點,我們稱這些「上一層節點」是該節點的「父
親」。現在給定一個樹狀圖資料,並給一個「目的地」節點名稱,請選手輸出從「樹根」連接
到目的地經過的所有節點。輸出資料的順序,應從「樹根」開始,一層一層向下,最後到達
「目的地」節點依序輸出,輸出的節點不能重覆。
輸入說明:第1 行表示共有多少個節點;第2 行是目的地節點;第3 行起是所有節點資料,
每行有一組符號以逗號隔開,第1 個符號為「節點名稱」,第2 個符號為其「父親名稱」。若
是「樹根」節點,其父親表示為「---」3 個連續減號。
輸出說明:列出從「樹根」連接到目的地經過的所有節點(包括樹根與目的地節點),而輸出
的節點間至少以1 個空白相隔開。
輸入範例:【檔名:in-2-2.txt】
11
K
A, ---
B, A
C, A
D, B
E, B
F, C
G, E
H, G
I, G
J, I
K, I
輸出範例:【檔名:out-2-2.txt】
A B E G I K
Problem 1文章的字母統計及單字的分離(99模擬)
Problem 1:文章的字母統計及單字的分離
選手請由輸入檔讀入一篇英文文章(文章內容包括「大、小寫英文」、「空白」及「標點符號」,
沒有任何「全型」字母或符號),並作以下的統計:
子題1(9%): 若不區別英文字母大小寫,請統計26 個英文字母A~Z在文章中出現的次數?
(只統計英文字母,其他如空白、標點符號等皆不統計。)
輸入說明:
第1 行表示文章的行數(行數至多10 行,每行最多120 個字),第2 行開始為文章的內容。
輸出說明:
第1 行分別列出字母A、B、C、D、E 及其統計次數,第2 行列出字母F、G、H、I、J 及其
統計次數,每行輸出5 個字母及統計,以此類推;但最後一行只列出字母Z 及其統計次數。
英文字母以「大寫」輸出,每個字母及其統計次數印在1 組小括號中,並由逗號分隔。
輸入範例:【檔名:in-1-1.txt】
4
Just ask a Chinese fruit farmer who now has to pay people to pollinate apple trees because there are no
longer enough bees to do the job. And it's not just the number of bees that are rapidly dwindling. As a
direct result of human activity, species are becoming extinct at a rate 1,000 times greater than the natural
average.
輸出範例:【檔名:out-1-1.txt】
(A, 27) (B, 6) (C, 7) (D, 6) (E, 38)
(F, 4) (G, 6) (H, 11) (I, 14) (J, 3)
(K, 1) (L, 9) (M, 5) (N, 16) (O, 16)
(P, 8) (Q, 0) (R, 18) (S, 15) (T, 28)
(U, 9) (V, 2) (W, 3) (X, 1) (Y, 3)
(Z, 0)
第 2 頁,共 8 頁
子題2(9%):請列出文章中使用那些「A」或「a」開頭的單字?
輸入說明:
第1 行表示文章的行數(行數至多10 行,每行最多120 個字),第2 行開始為文章的內容。
輸出說明:
依單字在文章中出現之順序,輸出開頭為「A」或「a」的單字。輸出的單字大小寫需保持與
原文章相同,而每行只輸出1 個單字。若同一單字多次出現在文章中,只有該單字在文章中
首次出現時才被輸出,第2 次或以後出現時均不再輸出。
輸入範例:【檔名:in-1-2.txt】
4
Just ask a Chinese fruit farmer who now has to pay people to pollinate apple trees because there are no
longer enough bees to do the job. And it's not just the number of bees that are rapidly dwindling. As a
direct result of human activity, species are becoming extinct at a rate 1,000 times greater than the natural
average.
輸出範例:【檔名:out-1-2.txt】
ask
a
apple
are
And
As
activity
at
average
選手請由輸入檔讀入一篇英文文章(文章內容包括「大、小寫英文」、「空白」及「標點符號」,
沒有任何「全型」字母或符號),並作以下的統計:
子題1(9%): 若不區別英文字母大小寫,請統計26 個英文字母A~Z在文章中出現的次數?
(只統計英文字母,其他如空白、標點符號等皆不統計。)
輸入說明:
第1 行表示文章的行數(行數至多10 行,每行最多120 個字),第2 行開始為文章的內容。
輸出說明:
第1 行分別列出字母A、B、C、D、E 及其統計次數,第2 行列出字母F、G、H、I、J 及其
統計次數,每行輸出5 個字母及統計,以此類推;但最後一行只列出字母Z 及其統計次數。
英文字母以「大寫」輸出,每個字母及其統計次數印在1 組小括號中,並由逗號分隔。
輸入範例:【檔名:in-1-1.txt】
4
Just ask a Chinese fruit farmer who now has to pay people to pollinate apple trees because there are no
longer enough bees to do the job. And it's not just the number of bees that are rapidly dwindling. As a
direct result of human activity, species are becoming extinct at a rate 1,000 times greater than the natural
average.
輸出範例:【檔名:out-1-1.txt】
(A, 27) (B, 6) (C, 7) (D, 6) (E, 38)
(F, 4) (G, 6) (H, 11) (I, 14) (J, 3)
(K, 1) (L, 9) (M, 5) (N, 16) (O, 16)
(P, 8) (Q, 0) (R, 18) (S, 15) (T, 28)
(U, 9) (V, 2) (W, 3) (X, 1) (Y, 3)
(Z, 0)
第 2 頁,共 8 頁
子題2(9%):請列出文章中使用那些「A」或「a」開頭的單字?
輸入說明:
第1 行表示文章的行數(行數至多10 行,每行最多120 個字),第2 行開始為文章的內容。
輸出說明:
依單字在文章中出現之順序,輸出開頭為「A」或「a」的單字。輸出的單字大小寫需保持與
原文章相同,而每行只輸出1 個單字。若同一單字多次出現在文章中,只有該單字在文章中
首次出現時才被輸出,第2 次或以後出現時均不再輸出。
輸入範例:【檔名:in-1-2.txt】
4
Just ask a Chinese fruit farmer who now has to pay people to pollinate apple trees because there are no
longer enough bees to do the job. And it's not just the number of bees that are rapidly dwindling. As a
direct result of human activity, species are becoming extinct at a rate 1,000 times greater than the natural
average.
輸出範例:【檔名:out-1-2.txt】
ask
a
apple
are
And
As
activity
at
average
2010年11月1日 星期一
身分證檢驗
內容 : 正體->简体
我國的身分證字號有底下這樣的規則,因此對於任意輸入的身分證字號可以有一些基本的判斷原則,請您來判斷一個身分證字號是否是正常的號碼(不代表確有此號、此人)。
(1) 英文代號以下表轉換成數字
A=10 台北市 J=18 新竹縣 S=26 高雄縣
B=11 台中市 K=19 苗栗縣 T=27 屏東縣
C=12 基隆市 L=20 台中縣 U=28 花蓮縣
D=13 台南市 M=21 南投縣 V=29 台東縣
E=14 高雄市 N=22 彰化縣 W=32 金門縣
F=15 台北縣 O=35 新竹市 X=30 澎湖縣
G=16 宜蘭縣 P=23 雲林縣 Y=31 陽明山
H=17 桃園縣 Q=24 嘉義縣 Z=33 連江縣
I=34 嘉義市 R=25 台南縣
(2) 英文轉成的數字, 個位數乘9再加上十位數的數字
(3) 各數字從右到左依次乘1、2、3、4....8
(4) 求出(2),(3) 及最後一碼的和
(5) (4)除10 若整除,則為 real,否則為 fake
例: T112663836
2 + 7*9 + 1*8 + 1*7 + 2*6 + 6*5 + 6*4 + 3*3 + 8*2 + 3*1 + 6 = 180
除以 10 整除,因此為 real
輸入說明 :
一組身分證號碼
輸出說明 :
輸出 real or fake
範例輸入 :
T112663836
S154287863
範例輸出 :
real
fake
我國的身分證字號有底下這樣的規則,因此對於任意輸入的身分證字號可以有一些基本的判斷原則,請您來判斷一個身分證字號是否是正常的號碼(不代表確有此號、此人)。
(1) 英文代號以下表轉換成數字
A=10 台北市 J=18 新竹縣 S=26 高雄縣
B=11 台中市 K=19 苗栗縣 T=27 屏東縣
C=12 基隆市 L=20 台中縣 U=28 花蓮縣
D=13 台南市 M=21 南投縣 V=29 台東縣
E=14 高雄市 N=22 彰化縣 W=32 金門縣
F=15 台北縣 O=35 新竹市 X=30 澎湖縣
G=16 宜蘭縣 P=23 雲林縣 Y=31 陽明山
H=17 桃園縣 Q=24 嘉義縣 Z=33 連江縣
I=34 嘉義市 R=25 台南縣
(2) 英文轉成的數字, 個位數乘9再加上十位數的數字
(3) 各數字從右到左依次乘1、2、3、4....8
(4) 求出(2),(3) 及最後一碼的和
(5) (4)除10 若整除,則為 real,否則為 fake
例: T112663836
2 + 7*9 + 1*8 + 1*7 + 2*6 + 6*5 + 6*4 + 3*3 + 8*2 + 3*1 + 6 = 180
除以 10 整除,因此為 real
輸入說明 :
一組身分證號碼
輸出說明 :
輸出 real or fake
範例輸入 :
T112663836
S154287863
範例輸出 :
real
fake
奇怪的老闆
內容 : 正體->简体
有一個很古怪的老闆,他有N名員工,每個人有自己的薪水,這個老闆很喜歡去找出編號第A到編號到B之間的最高薪水與最低薪水的差,但是你以為他只找一次嗎?當然不是,他有強迫症,他每隔1秒就隨機寫兩個數字,然後找出這段數字裡最多薪水的錢,並寫下來作成紀錄。
老闆每次都要他的秘書幫他找,他的秘書受不了,想請你幫她寫一個程式讓他可以很迅速的找到,在這區間最高薪水與最低薪水的差是多少錢, 好讓他可以輕鬆一下。
輸入說明 :
第一行有兩個數字N(1 ≤ N ≤ 50,000), Q (1 ≤ Q ≤ 200,000) 代表有N名員工跟Q個問題。
接下來有 N行代表第1~N名的員工薪水。
在接下來的Q行有兩個數字 a,b
"(0 < a < = b < = n)" 代表老闆寫的兩個數字,請你找出這段區間的最高薪水與最低薪水的差。
輸出說明 :
對於每一個問題,印出最高薪水與最低薪水的差為何?並換行。
範例輸入 :
6 3
1
7
3
4
2
5
1 5
4 6
2 2
範例輸出 :
6
3
0
有一個很古怪的老闆,他有N名員工,每個人有自己的薪水,這個老闆很喜歡去找出編號第A到編號到B之間的最高薪水與最低薪水的差,但是你以為他只找一次嗎?當然不是,他有強迫症,他每隔1秒就隨機寫兩個數字,然後找出這段數字裡最多薪水的錢,並寫下來作成紀錄。
老闆每次都要他的秘書幫他找,他的秘書受不了,想請你幫她寫一個程式讓他可以很迅速的找到,在這區間最高薪水與最低薪水的差是多少錢, 好讓他可以輕鬆一下。
輸入說明 :
第一行有兩個數字N(1 ≤ N ≤ 50,000), Q (1 ≤ Q ≤ 200,000) 代表有N名員工跟Q個問題。
接下來有 N行代表第1~N名的員工薪水。
在接下來的Q行有兩個數字 a,b
"(0 < a < = b < = n)" 代表老闆寫的兩個數字,請你找出這段區間的最高薪水與最低薪水的差。
輸出說明 :
對於每一個問題,印出最高薪水與最低薪水的差為何?並換行。
範例輸入 :
6 3
1
7
3
4
2
5
1 5
4 6
2 2
範例輸出 :
6
3
0
數字合併
內容 : 正體->简体
黑板上有n個數字寫成一排,現在每次選擇兩個相鄰的數字,把比較小的那個 數字擦掉(如果兩個數字一樣大,那麼擦掉任何一個都可以。)然而,這些步驟需要花費,這個花費恰好等於留下來的那個數字(比較大的那個)。
請問經過n-1次操作,黑板上會剩下的那個數字是多少?
你以為問題這麼簡單嗎?錯!
真正的問題是:
請問經過n-1次操作,黑板上會剩下最大的那個數字,所有操作方法中,最小總花費是多少?
輸入說明 :
輸入檔只包含一筆測試資料。
第一列有一個正整數n(1<=n<=1,000,000)代表黑板上數字的個數。
接下來有n列,每列有一個正整數(1<=數字<=109)依序代表黑板上的每個數字。
輸出說明 :
請輸出經過n-1次操作之後,所需的最小總花費。
範例輸入 :
5
7
4
5
2
5
範例輸出 :
22
提示 :
消掉4、花費5;
消掉2、花費5;
消掉5、花費5;
消掉5、花費7;
總花費是5+5+5+7=22。
黑板上有n個數字寫成一排,現在每次選擇兩個相鄰的數字,把比較小的那個 數字擦掉(如果兩個數字一樣大,那麼擦掉任何一個都可以。)然而,這些步驟需要花費,這個花費恰好等於留下來的那個數字(比較大的那個)。
請問經過n-1次操作,黑板上會剩下的那個數字是多少?
你以為問題這麼簡單嗎?錯!
真正的問題是:
請問經過n-1次操作,黑板上會剩下最大的那個數字,所有操作方法中,最小總花費是多少?
輸入說明 :
輸入檔只包含一筆測試資料。
第一列有一個正整數n(1<=n<=1,000,000)代表黑板上數字的個數。
接下來有n列,每列有一個正整數(1<=數字<=109)依序代表黑板上的每個數字。
輸出說明 :
請輸出經過n-1次操作之後,所需的最小總花費。
範例輸入 :
5
7
4
5
2
5
範例輸出 :
22
提示 :
消掉4、花費5;
消掉2、花費5;
消掉5、花費5;
消掉5、花費7;
總花費是5+5+5+7=22。
Colorful Board
內容 : 正體->简体
給你一個板子,在上面M條水平線跟N條垂直線,因此在整個板子有(M+1) x (N+1)格子,現在請你在每個格子上填上顏色,總共有4種顏色Red,Green,Blue,Orange。
為了使板子更加漂亮,你必須小心一件事情,兩鄰的格子不能有相同的顏色(相鄰的定義是有共同的邊),但是有些格子是被禁止塗上任何顏色的,題目來了,你必須回答有幾種方式可以塗完,但不觸犯以上規則。
輸入說明 :
第一個數字T(T<=50)代表有幾組冊資,每一組測資會給兩格數字M,N ( 0 < M , N < = 6 )代表有幾條水平線跟垂直線,下一行但表有幾格被禁止不能圖畫的個數K( 0 < = K < = ( M + 1 ) * ( N + 1 ) ),接下來K行會包含兩個數字X,Y (1<=x<=M+1, 1<=y<=N+1),代表第X行的第Y個是被禁止塗畫。
輸出說明 :
對於每一個測資,請輸出一行 "Case #K: P",K代表第幾組測試資料,P代表有幾種可能,由於答案可能很大,請mod 1000000007
範例輸入 :
2
1 1
1
2 1
0 0
0
範例輸出 :
Case 1: 36
Case 2: 4
給你一個板子,在上面M條水平線跟N條垂直線,因此在整個板子有(M+1) x (N+1)格子,現在請你在每個格子上填上顏色,總共有4種顏色Red,Green,Blue,Orange。
為了使板子更加漂亮,你必須小心一件事情,兩鄰的格子不能有相同的顏色(相鄰的定義是有共同的邊),但是有些格子是被禁止塗上任何顏色的,題目來了,你必須回答有幾種方式可以塗完,但不觸犯以上規則。
輸入說明 :
第一個數字T(T<=50)代表有幾組冊資,每一組測資會給兩格數字M,N ( 0 < M , N < = 6 )代表有幾條水平線跟垂直線,下一行但表有幾格被禁止不能圖畫的個數K( 0 < = K < = ( M + 1 ) * ( N + 1 ) ),接下來K行會包含兩個數字X,Y (1<=x<=M+1, 1<=y<=N+1),代表第X行的第Y個是被禁止塗畫。
輸出說明 :
對於每一個測資,請輸出一行 "Case #K: P",K代表第幾組測試資料,P代表有幾種可能,由於答案可能很大,請mod 1000000007
範例輸入 :
2
1 1
1
2 1
0 0
0
範例輸出 :
Case 1: 36
Case 2: 4
2010年10月29日 星期五
戰艦謎題
內容 :
在一個2x2的格子圖形中,有三艘各佔一個格子的戰艦,戰艦的位置均在格子的範圍內。三艘戰艦重量皆不同,從1噸到3噸各有一艘,因為大霧瀰漫不知正確位置,僅知道每一列與每一行的總重量,請問聰明的你,知道每一艘戰艦的正確位置嗎?
舉例來說,如果我們知道每一列與每一行的總重量如下圖:
囗囗5
囗囗1
42
那麼這個戰艦謎題的一組正確答案如下圖:
325
101
42
注意:我們給的輸入資料不一定只有一組正確答案,這時候你只需輸出其中一組正確答案即可。此外,我們給的輸入資料有可能沒有正確的答案,這時候只需輸出"No solutions."即可。
輸入說明 :
總共有四個整數,每個數值間以一個空白字元隔開,這些數字個值均介於0到5之間。前2個整數依序表示每一列(row)的總重量,接下來的2個整數依序表示每一行(column)的總重量。
輸出說明 :
請輸出4個整數,分成兩列,每列含有2個整數,整數中間以一個空白隔開,表示2x2的格子中,停在每個位置的戰艦重量。其中以0表示沒有戰艦。(範例一就是上圖的例子)如果沒有解答請輸出 "No solutions."
範例輸入 :
輸入範例一:
5 1 4 2
輸入範例二:
3 3 1 5
輸入範例三:
3 2 3 4
範例輸出 :
輸出範例一:
3 2 1 0
輸出範例二:
0 3 1 2
輸出範例三:
No solutions.
在一個2x2的格子圖形中,有三艘各佔一個格子的戰艦,戰艦的位置均在格子的範圍內。三艘戰艦重量皆不同,從1噸到3噸各有一艘,因為大霧瀰漫不知正確位置,僅知道每一列與每一行的總重量,請問聰明的你,知道每一艘戰艦的正確位置嗎?
舉例來說,如果我們知道每一列與每一行的總重量如下圖:
囗囗5
囗囗1
42
那麼這個戰艦謎題的一組正確答案如下圖:
325
101
42
注意:我們給的輸入資料不一定只有一組正確答案,這時候你只需輸出其中一組正確答案即可。此外,我們給的輸入資料有可能沒有正確的答案,這時候只需輸出"No solutions."即可。
輸入說明 :
總共有四個整數,每個數值間以一個空白字元隔開,這些數字個值均介於0到5之間。前2個整數依序表示每一列(row)的總重量,接下來的2個整數依序表示每一行(column)的總重量。
輸出說明 :
請輸出4個整數,分成兩列,每列含有2個整數,整數中間以一個空白隔開,表示2x2的格子中,停在每個位置的戰艦重量。其中以0表示沒有戰艦。(範例一就是上圖的例子)如果沒有解答請輸出 "No solutions."
範例輸入 :
輸入範例一:
5 1 4 2
輸入範例二:
3 3 1 5
輸入範例三:
3 2 3 4
範例輸出 :
輸出範例一:
3 2 1 0
輸出範例二:
0 3 1 2
輸出範例三:
No solutions.
海藻(algae)
內容 :
根據最新的生態學研究報導,在台北市植物園的蓮花池中,發現了一種奇特的海藻,此種海藻的外形具有一種十 分特殊的性質:
種子落地後,經過一天的時間,會先長出一根長一公分的綠色分枝。
綠色的分枝,經過一天的時間後,會向上成長一公分,並且變成黃色。
黃色的分枝,經過一天的時間後,會向上成長一公分,並且分成左右兩個分枝,其中左分枝為綠色,右分枝為黃色。
所有的分枝都不會互相交錯,同時恰好成長在同一個平面上。
舉例來說,若我們由左而右俯視觀察此海藻每天的生長情形,則在種子落地後的第一天,觀察結果為『綠』,第 二天的觀察結果為『黃』,第三天的觀察結果為『綠黃』,第四天的觀察結果為『黃綠黃』, 第五天的觀察結果為『綠黃黃綠黃』,依此類推。
請寫一個程式,預測在第 N 天時,由左邊數來第 K 個分枝的顏色為何。
輸入說明 :
每個測資點中的第一行有一個正整數 M 代表此測資點中共有 M 組測試資料
每組測試資料含有兩個以空白相間隔的正整數,分別依次為 N 與 K
為方便起見,所有的測試資料皆滿足 0 < M < 100,0 < N < 100 且 0 < K < 2000000000
輸出說明 :
每行輸出第 N 天時
由左邊數來第 K 個分枝的顏色(請用數字 0 代表綠色,1 代表黃色)
若第 N 天時,此海藻的分枝數少於 K,則輸出 -1
範例輸入 :
3
3 1
5 5
6 100
範例輸出 :
0
1
-1
根據最新的生態學研究報導,在台北市植物園的蓮花池中,發現了一種奇特的海藻,此種海藻的外形具有一種十 分特殊的性質:
種子落地後,經過一天的時間,會先長出一根長一公分的綠色分枝。
綠色的分枝,經過一天的時間後,會向上成長一公分,並且變成黃色。
黃色的分枝,經過一天的時間後,會向上成長一公分,並且分成左右兩個分枝,其中左分枝為綠色,右分枝為黃色。
所有的分枝都不會互相交錯,同時恰好成長在同一個平面上。
舉例來說,若我們由左而右俯視觀察此海藻每天的生長情形,則在種子落地後的第一天,觀察結果為『綠』,第 二天的觀察結果為『黃』,第三天的觀察結果為『綠黃』,第四天的觀察結果為『黃綠黃』, 第五天的觀察結果為『綠黃黃綠黃』,依此類推。
請寫一個程式,預測在第 N 天時,由左邊數來第 K 個分枝的顏色為何。
輸入說明 :
每個測資點中的第一行有一個正整數 M 代表此測資點中共有 M 組測試資料
每組測試資料含有兩個以空白相間隔的正整數,分別依次為 N 與 K
為方便起見,所有的測試資料皆滿足 0 < M < 100,0 < N < 100 且 0 < K < 2000000000
輸出說明 :
每行輸出第 N 天時
由左邊數來第 K 個分枝的顏色(請用數字 0 代表綠色,1 代表黃色)
若第 N 天時,此海藻的分枝數少於 K,則輸出 -1
範例輸入 :
3
3 1
5 5
6 100
範例輸出 :
0
1
-1
2010年10月28日 星期四
最長共同字串
內容 :
序列1:
序列 2:
給你2個字串,請你輸出他們的最長共同子字串(longest common subsequence)的長度。例如:給你以下2個字串:
abcdgh
aedfhr
他們的最長共同子字串為adh,長度為3。
輸入說明 :
輸入含有多組測試資料。每一組測試資料2列,分別代表這2個字串(最多1000個字元)。
輸出說明 :
每組測試資料輸出他們的最長共同子字串(longest common subsequence)的長度。
範例輸入 :
a1b2c3d4e
zz1yy2xx3ww4vv
abcdgh
aedfhr
abcdefghijklmnopqrstuvwxyz
a0b0c0d0e0f0g0h0i0j0k0l0m0n0o0p0q0r0s0t0u0v0w0x0y0z0
abcdefghijklmnzyxwvutsrqpo
opqrstuvwxyzabcdefghijklmn
範例輸出 :
4
3
26
14
序列1:
序列 2:
給你2個字串,請你輸出他們的最長共同子字串(longest common subsequence)的長度。例如:給你以下2個字串:
abcdgh
aedfhr
他們的最長共同子字串為adh,長度為3。
輸入說明 :
輸入含有多組測試資料。每一組測試資料2列,分別代表這2個字串(最多1000個字元)。
輸出說明 :
每組測試資料輸出他們的最長共同子字串(longest common subsequence)的長度。
範例輸入 :
a1b2c3d4e
zz1yy2xx3ww4vv
abcdgh
aedfhr
abcdefghijklmnopqrstuvwxyz
a0b0c0d0e0f0g0h0i0j0k0l0m0n0o0p0q0r0s0t0u0v0w0x0y0z0
abcdefghijklmnzyxwvutsrqpo
opqrstuvwxyzabcdefghijklmn
範例輸出 :
4
3
26
14
Lotto
內容 : 正體->简体
為了呼應台灣電腦彩券的發行,我們再次推出跟組合有關的題目。你在買彩券的時候一定會挑你喜歡的數字吧!(雖然理論上不會增加你的中獎機率,但是你還是會選擇你的Lucky Number)我們的問題是:假設共有49個號碼,而你必須在你的 k (k>6)個Lucky Number中挑6個號碼作為一張彩券的數字組合。例如:你的Lucky Number的集合是{1,2,3,5,8,13,21,34}以就是說 k=8 ,那麼你就有C(8,6)=28種可能的彩券組合:
[1,2,3,5,8,13], [1,2,3,5,8,21], [1,2,3,5,8,34], [1,2,3,5,13,21], ..., [3,5,8,13,21,34].
你的任務是讀入k以及Lucky Number的集合,然後輸出所有可能的組合。
輸入說明 :
每筆測試資料一行,每行的第1個整數代表 k( 6 < k < 1 3 ) 。 接下來的k個整數代表Lucky Number的集合,此集合已經按數字由小到大排好。k=0代表輸入結束。
輸出說明 :
對每一筆測試資料,輸出其所有可能的組合,每個組合一行。請注意輸出組合的順序需由小到大排列。測試資料之間請空一行。請參考Sample Output。
範例輸入 :
7 1 2 3 4 5 6 7
8 1 2 3 5 8 13 21 34
0
範例輸出 :
1 2 3 4 5 6
1 2 3 4 5 7
1 2 3 4 6 7
1 2 3 5 6 7
1 2 4 5 6 7
1 3 4 5 6 7
2 3 4 5 6 7
1 2 3 5 8 13
1 2 3 5 8 21
1 2 3 5 8 34
1 2 3 5 13 21
1 2 3 5 13 34
1 2 3 5 21 34
1 2 3 8 13 21
1 2 3 8 13 34
1 2 3 8 21 34
1 2 3 13 21 34
1 2 5 8 13 21
1 2 5 8 13 34
1 2 5 8 21 34
1 2 5 13 21 34
1 2 8 13 21 34
1 3 5 8 13 21
1 3 5 8 13 34
1 3 5 8 21 34
1 3 5 13 21 34
1 3 8 13 21 34
1 5 8 13 21 34
2 3 5 8 13 21
2 3 5 8 13 34
2 3 5 8 21 34
2 3 5 13 21 34
2 3 8 13 21 34
2 5 8 13 21 34
3 5 8 13 21 34
為了呼應台灣電腦彩券的發行,我們再次推出跟組合有關的題目。你在買彩券的時候一定會挑你喜歡的數字吧!(雖然理論上不會增加你的中獎機率,但是你還是會選擇你的Lucky Number)我們的問題是:假設共有49個號碼,而你必須在你的 k (k>6)個Lucky Number中挑6個號碼作為一張彩券的數字組合。例如:你的Lucky Number的集合是{1,2,3,5,8,13,21,34}以就是說 k=8 ,那麼你就有C(8,6)=28種可能的彩券組合:
[1,2,3,5,8,13], [1,2,3,5,8,21], [1,2,3,5,8,34], [1,2,3,5,13,21], ..., [3,5,8,13,21,34].
你的任務是讀入k以及Lucky Number的集合,然後輸出所有可能的組合。
輸入說明 :
每筆測試資料一行,每行的第1個整數代表 k( 6 < k < 1 3 ) 。 接下來的k個整數代表Lucky Number的集合,此集合已經按數字由小到大排好。k=0代表輸入結束。
輸出說明 :
對每一筆測試資料,輸出其所有可能的組合,每個組合一行。請注意輸出組合的順序需由小到大排列。測試資料之間請空一行。請參考Sample Output。
範例輸入 :
7 1 2 3 4 5 6 7
8 1 2 3 5 8 13 21 34
0
範例輸出 :
1 2 3 4 5 6
1 2 3 4 5 7
1 2 3 4 6 7
1 2 3 5 6 7
1 2 4 5 6 7
1 3 4 5 6 7
2 3 4 5 6 7
1 2 3 5 8 13
1 2 3 5 8 21
1 2 3 5 8 34
1 2 3 5 13 21
1 2 3 5 13 34
1 2 3 5 21 34
1 2 3 8 13 21
1 2 3 8 13 34
1 2 3 8 21 34
1 2 3 13 21 34
1 2 5 8 13 21
1 2 5 8 13 34
1 2 5 8 21 34
1 2 5 13 21 34
1 2 8 13 21 34
1 3 5 8 13 21
1 3 5 8 13 34
1 3 5 8 21 34
1 3 5 13 21 34
1 3 8 13 21 34
1 5 8 13 21 34
2 3 5 8 13 21
2 3 5 8 13 34
2 3 5 8 21 34
2 3 5 13 21 34
2 3 8 13 21 34
2 5 8 13 21 34
3 5 8 13 21 34
電費系統
內容 : 正體->简体
假設你身為一個台電工程師,你正要為 GOGO 百貨的電梯設計一套電費計算系統,來計算GOGO 百貨的電梯每天所耗的電費是多少。已知電梯所耗的電力會和它所運作的樓層成正比,但是電梯下樓比上樓要省電。所以想請你根據下面這個規則,設計一套電費計算系統。
(1) 電梯上樓時,每經過一個樓層,要花電費 20 元。
(2) 電梯下樓時,每經過一個樓層,要花電費 10 元。
(3) 你可以假設電梯停在某一個樓層時不會耗電。
舉例來說:今天有一個電梯從2 樓到8 樓再到5 樓,則所耗的電費為:從2樓到8 樓,所耗的電費是(8-2) x 20 = 120 元。電梯從8 樓到5 樓,所耗的電費是(8-5) x 10 = 30 元。所以總共花了150 元。
輸入說明 :
輸入檔中會有多筆資料,第一行是一個整數 N(1
輸入測資中的電梯樓層最高不會超過 101 樓。
輸出說明 :
請根據電梯上下運作的樓層,計算出在一日中電梯運作所花的電費。(為了節能減碳,每日電費最高不會超過10,000 元。)
範例輸入 :
3
2 8 5
7
2 9 7 3 4 6 1
0
範例輸出 :
150
310
假設你身為一個台電工程師,你正要為 GOGO 百貨的電梯設計一套電費計算系統,來計算GOGO 百貨的電梯每天所耗的電費是多少。已知電梯所耗的電力會和它所運作的樓層成正比,但是電梯下樓比上樓要省電。所以想請你根據下面這個規則,設計一套電費計算系統。
(1) 電梯上樓時,每經過一個樓層,要花電費 20 元。
(2) 電梯下樓時,每經過一個樓層,要花電費 10 元。
(3) 你可以假設電梯停在某一個樓層時不會耗電。
舉例來說:今天有一個電梯從2 樓到8 樓再到5 樓,則所耗的電費為:從2樓到8 樓,所耗的電費是(8-2) x 20 = 120 元。電梯從8 樓到5 樓,所耗的電費是(8-5) x 10 = 30 元。所以總共花了150 元。
輸入說明 :
輸入檔中會有多筆資料,第一行是一個整數 N(1
輸入測資中的電梯樓層最高不會超過 101 樓。
輸出說明 :
請根據電梯上下運作的樓層,計算出在一日中電梯運作所花的電費。(為了節能減碳,每日電費最高不會超過10,000 元。)
範例輸入 :
3
2 8 5
7
2 9 7 3 4 6 1
0
範例輸出 :
150
310
科學記號
內容 : 正體->简体
科學上採用的數字常寫成 a × 10n 的形式﹐其中 1 ≤ a < 10﹐n 是整數﹐
例如:(一) 光速是每秒 300,000,000 公尺﹐若取一位有效數字,
記為 3 × 108 公尺/秒。
(二) 電子的質量是0.000,000,000,000,000,000,000,000,000,909 公克,
若取二位有效數字,記為 9.1 × 10-28 公克。
輸入說明 :
輸入檔中有多筆測試資料。每筆測試資料第一行有一個正整數 N, (1 ≦ N ≦ 100),代表有N筆測試資料。
接下來,有N行,每行有二個數字,第二數字表示取幾位有效數字。
須四捨五入!
輸出說明 :
對於每筆測資,輸出一行此筆資料的科學記號。
範例輸入 :
2
300,000,000 4
0.000,000,000,000,000,000,000,000,000,909 2
範例輸出 :
3.000x10(8)
9.1x10(-28)
科學上採用的數字常寫成 a × 10n 的形式﹐其中 1 ≤ a < 10﹐n 是整數﹐
例如:(一) 光速是每秒 300,000,000 公尺﹐若取一位有效數字,
記為 3 × 108 公尺/秒。
(二) 電子的質量是0.000,000,000,000,000,000,000,000,000,909 公克,
若取二位有效數字,記為 9.1 × 10-28 公克。
輸入說明 :
輸入檔中有多筆測試資料。每筆測試資料第一行有一個正整數 N, (1 ≦ N ≦ 100),代表有N筆測試資料。
接下來,有N行,每行有二個數字,第二數字表示取幾位有效數字。
須四捨五入!
輸出說明 :
對於每筆測資,輸出一行此筆資料的科學記號。
範例輸入 :
2
300,000,000 4
0.000,000,000,000,000,000,000,000,000,909 2
範例輸出 :
3.000x10(8)
9.1x10(-28)
2010年10月27日 星期三
2010年10月26日 星期二
隔熱紙
內容 :
喵嗚建設公司最近由北到南蓋了一整排共n棟的大樓,且每棟大樓是緊緊貼在一起的
而喵嗚建設公司希望能夠帶給住戶舒適的住宅環境,因此決定在東面窗上貼滿隔熱紙
然而預算有限,不能有任何隔熱紙被浪費,又切割隔熱紙是一向充滿麻煩的工程
你可以幫喵嗚建設公司算出至少要幾張矩形的隔熱紙才能貼滿整排大樓的東側嗎?
輸入說明 :
第一行有一個正整數 n(n<=100000),代表有幾棟大樓
接下來n行每行有兩個正整數(<=1,000,000,000),依序代表每棟大樓的寬度及高度
輸出說明 :
輸出最少所需要的隔熱紙數
範例輸入 :
5
1 2
1 3
2 2
2 5
1 4
範例輸出 :
4
喵嗚建設公司最近由北到南蓋了一整排共n棟的大樓,且每棟大樓是緊緊貼在一起的
而喵嗚建設公司希望能夠帶給住戶舒適的住宅環境,因此決定在東面窗上貼滿隔熱紙
然而預算有限,不能有任何隔熱紙被浪費,又切割隔熱紙是一向充滿麻煩的工程
你可以幫喵嗚建設公司算出至少要幾張矩形的隔熱紙才能貼滿整排大樓的東側嗎?
輸入說明 :
第一行有一個正整數 n(n<=100000),代表有幾棟大樓
接下來n行每行有兩個正整數(<=1,000,000,000),依序代表每棟大樓的寬度及高度
輸出說明 :
輸出最少所需要的隔熱紙數
範例輸入 :
5
1 2
1 3
2 2
2 5
1 4
範例輸出 :
4
畢業旅行
內容 :
多年來友情的羈絆,終於將在這畢業的季節開花結果。
這幾天,班上同學們無時無刻都熱烈討論著畢業旅行的地點。
小明說,如果要去六福村,可以順便去小人國;
小美說,如果去了恆春的話,墾丁就在幾十公里外了,一定也要去玩;
小華表示,小鬼湖跟大鬼湖好像很近,似乎都是很有趣的地方。
身為班長,聽到同學這麼多「去了哪裡也可以去哪裡」的資訊後,
你決定要為班上的同學們,找到一個能玩最多景點的畢業旅行。
輸入說明 :
有多組測試資料,以 EOF 結束。
每組測試資料的第一行有兩個正整數 n (n<=1000000) 和 m (m<=100000),
表示景點有 n 個,編號為 0 ~ n-1。
接下來有 m 行,每行有兩個整數 a 和 b (0<=a,b
輸出說明 :
輸出一個數字,表示畢業旅行最多可以玩的景點數量。
範例輸入 :
6 4
0 1
2 3
1 3
5 4
1000000 0
1000000 1
0 999999
範例輸出 :
4
1
2
多年來友情的羈絆,終於將在這畢業的季節開花結果。
這幾天,班上同學們無時無刻都熱烈討論著畢業旅行的地點。
小明說,如果要去六福村,可以順便去小人國;
小美說,如果去了恆春的話,墾丁就在幾十公里外了,一定也要去玩;
小華表示,小鬼湖跟大鬼湖好像很近,似乎都是很有趣的地方。
身為班長,聽到同學這麼多「去了哪裡也可以去哪裡」的資訊後,
你決定要為班上的同學們,找到一個能玩最多景點的畢業旅行。
輸入說明 :
有多組測試資料,以 EOF 結束。
每組測試資料的第一行有兩個正整數 n (n<=1000000) 和 m (m<=100000),
表示景點有 n 個,編號為 0 ~ n-1。
接下來有 m 行,每行有兩個整數 a 和 b (0<=a,b
輸出說明 :
輸出一個數字,表示畢業旅行最多可以玩的景點數量。
範例輸入 :
6 4
0 1
2 3
1 3
5 4
1000000 0
1000000 1
0 999999
範例輸出 :
4
1
2
2010年10月25日 星期一
Find the Telephone
內容 : 正體->简体
有些地方會用對應的字母來代替數字使得電話號碼更好記。如此一來 MY LOVE 就代表 69 5683。這不是萬靈丹,因為有的電話號碼並不能構成一個字或片語,而且 1 和 0 沒有對應的字母。
請讀入一個字串並依據下表轉成電話號碼。字串由大寫字母 (A-Z)、連字號(-) 和數字 1 和 0 所組成。
請讀入一個字串並依據下表轉成電話號碼。字串由大寫字母 (A-Z)、連字號(-) 和數字 1 和 0 所組成。
| 字母 | 數字 |
| ABC | 2 |
| DEF | 3 |
| GHI | 4 |
| JKL | 5 |
| MNO | 6 |
| PQRS | 7 |
| TUV | 8 |
| WXYZ | 9 |
輸入說明 :
輸入含有若干字串。每個字串單獨在一行,有 C 個字元,1 ≤ C ≤ 30 。輸入以 EOF 作為結束。
輸出說明 :
對於每個字串,請輸出相對應的電話號碼。
範例輸入 :

1-HOME-SWEET-HOME
MY-MISERABLE-JOB
範例輸出 :
1-4663-79338-4663
69-647372253-562
No Problem
內容 :
最近程式競賽非常頻繁。儘管對參賽者來說這是好事,對出題者來說卻適得其反。目前出題者尚能維持一個題庫並說:「沒有問題!」但是如果繼續這樣下去不知道還能維持多久。
給你一年中每個月所出的題目數量及每個月所需要的題目數量。如果某個月需要 N 個題目,而當時的題庫數量不足,那麼該月的所有比賽均取消。請寫個程式來判斷是否有足夠的題目來辦比賽。記住,如果某個題目是在 X 月出的,該題目必須在 X+1 月或其後的月份才能使用。
給你一年中每個月所出的題目數量及每個月所需要的題目數量。如果某個月需要 N 個題目,而當時的題庫數量不足,那麼該月的所有比賽均取消。請寫個程式來判斷是否有足夠的題目來辦比賽。記住,如果某個題目是在 X 月出的,該題目必須在 X+1 月或其後的月份才能使用。
輸入說明 :
每筆測資的第一行有一個整數 S (0≤S≤100),表示年初已有的庫存題目數量。第二行有 12 個以空白隔開的整數,依序表示一到十二月每個月所出的題目數量。第三行也有 12 個以空白隔開的整數,依序表示每個月比賽所需要的題目數量。這些整數會介於 0 到 20 之間 (含)。負數代表輸入的結束。
輸出說明 :
對於每筆測資,印出一行 "Case X:",X 代表測資編號。然後印出 12 行,如果 i 月 (1≤i≤12) 有足夠的題目,則在第 i 行印出"No problem! :D" (沒有問題),否則印出 "No problem. :(" (沒有題目)。
範例輸入 :
5
3 0 3 5 8 2 1 0 3 5 6 9
0 0 10 2 6 4 1 0 1 1 2 2
-1
範例輸出 :
Case 1:
No problem! :D
No problem! :D
No problem. :(
No problem! :D
No problem! :D
No problem! :D
No problem! :D
No problem! :D
No problem! :D
No problem! :D
No problem! :D
No problem! :D
提示 :雖然這個題目最好用「陣列」來解,但是不用陣列也可以解,只是程式碼會重覆且冗長。Alarm Clock
內容 :
Daniela 在一家大醫院當護士,工作時間常變來變去。更糟的是她睡得很沉,鬧鐘很難叫醒她。
最近她收到了一個有多種鬧鈴聲的數位時鐘,希望它可以解決她的問題。由於近來較為疲累,她希望善用休息時間。她隨身帶著這個鬧鐘,只要有休息時間,她就設好該醒來的時間並試著入睡。不過當她越焦急地想睡著,她越是睡不著。
她一直苦惱地想知道如果她可以立刻睡著,在鬧鐘響以前她可以有幾分鐘的睡眠。但是她的算術不好,所以請你寫一個程式,根據現在的時間及鬧鈴的時間算出她可以睡幾分鐘。
最近她收到了一個有多種鬧鈴聲的數位時鐘,希望它可以解決她的問題。由於近來較為疲累,她希望善用休息時間。她隨身帶著這個鬧鐘,只要有休息時間,她就設好該醒來的時間並試著入睡。不過當她越焦急地想睡著,她越是睡不著。
她一直苦惱地想知道如果她可以立刻睡著,在鬧鐘響以前她可以有幾分鐘的睡眠。但是她的算術不好,所以請你寫一個程式,根據現在的時間及鬧鈴的時間算出她可以睡幾分鐘。
輸入說明 :
輸入含有多筆測資,每筆測資一行,含有四個整數 h1、m1、h2 及 m2,h1:m1代表現在的時與分,h2:m2則代表鬧鈴所設的時間 (時與分),(0≤h1≤23, 0≤m1≤59, 0≤h2≤23, 0≤m2≤59)。
最後一行含有四個以空格分開的 0,代表輸入的結束。
最後一行含有四個以空格分開的 0,代表輸入的結束。
輸出說明 :
對於每筆測資,你的程式要把 Daniela 可以睡的分鐘數單獨輸出於一行。
範例輸入 :
1 5 3 5
23 59 0 34
21 33 21 10
0 0 0 0
範例輸出 :
120
35
1417
Fibonacci numbers
內容 : 正體->简体
費氏數列的處理,一向都是相當地費事。當然今天也不例外。各 位應該有聽說過費式數列,或許沒有聽過以費式數列為基底的數字表示法吧!費氏數列基本上就是 (1,1,2,3,5,8,...),定義第零項、第一項都是1,自第二項起,每一項的數值皆等於前兩項的和。接下來我們來考慮費氏進位制:
說得單純一些,就是我們考慮將一個正整數 X 表示成費氏數列當中某些不重複項的和。例如
35 = 1 + 34 = 1 + 13 + 21 = 1 + 5 + 8 + 21 = 1 + 2 + 3 + 8 + 21
看起來有很多種表示法對吧?但若我們規定「選出來的數字不能有相鄰的項」,那麼一切就會變得簡單些了,例如:
35 = 1 + 34
30 = 1 + 8 + 21
28 = 2 + 5 + 21
12 = 1 + 3 + 8
7 = 2 + 5
巧合的是,可以證明恰好只有一種這樣的表示方法。
我們可以用類似二進位數的方法來表達這樣的一個正整數在「費氏進位制」底下長的樣子。
不過,現在費事的地方來了,我們要怎麼樣對兩個「費氏進位」的數字作加法呢?
這就是你的工作,給你兩個以費氏進位制 的數字,你必須把他們加起來,並且用費氏進位制表示出來。
說得單純一些,就是我們考慮將一個正整數 X 表示成費氏數列當中某些不重複項的和。例如
35 = 1 + 34 = 1 + 13 + 21 = 1 + 5 + 8 + 21 = 1 + 2 + 3 + 8 + 21
看起來有很多種表示法對吧?但若我們規定「選出來的數字不能有相鄰的項」,那麼一切就會變得簡單些了,例如:
35 = 1 + 34
30 = 1 + 8 + 21
28 = 2 + 5 + 21
12 = 1 + 3 + 8
7 = 2 + 5
巧合的是,可以證明恰好只有一種這樣的表示方法。
我們可以用類似二進位數的方法來表達這樣的一個正整數在「費氏進位制」底下長的樣子。
不過,現在費事的地方來了,我們要怎麼樣對兩個「費氏進位」的數字作加法呢?
這就是你的工作,給你兩個以費氏進位制 的數字,你必須把他們加起來,並且用費氏進位制表示出來。
輸入說明 :
每兩行為一組測資,每個長度不會超過100個,每組測資以空白隔開
輸出說明 :
請輸出結果,並每兩組之間空一行隔開
範例輸入 :
10010
1
10000
1000
10000
10000
範例輸出 :
10100
100000
100100
Number Transformation
內容 :
給你一個數字S,你可以將A轉換成B藉由加上一個X,X是一個A的質因數(1跟A不考慮進去),現在你的工作就是找出最少需要轉換次數把S轉換成T
EX: 6 12
6->9->12 2次
6->8-> 10->12 3次
EX: 6 12
6->9->12 2次
6->8-> 10->12 3次
輸入說明 :
每組測資都有兩的數字S (1<=S<=100) & T (1<=T<=1000),
兩個0代表結束,不用輸出任何數字 。
兩個0代表結束,不用輸出任何數字 。
輸出說明 :
對於每個一個測資,除了0 0以外 ,請應出 “Case X: Y”,X從1開始算起,Y為S轉換到T的最小次數,若是無法轉換成功請書出-1
範例輸入 :

6 12
6 13
0 0
範例輸出 :
Case 1: 2
Case 2: -1
2010年10月22日 星期五
棒球九宮格
內容 :
小明很喜歡棒球。某天晚上跟媽媽到家裡附近逛夜市,突然發現多了一個棒球九宮格的遊戲攤位(如圖一)。遊戲規則如下:一開始九宮格內會分別擺上一個木板,玩家站在距離九宮格板數公尺外,總共可以丟出九顆球。被命中的格子裡的木板會倒下;若球丟出範圍外,或是剛好丟在九宮格的框架上,則所有格子都會維持原樣。一旦將球丟出去,可用的球數就減少一,直到將九顆球丟完為止。

九顆球都丟完之後,夜市的老闆會根據倒下的格子來檢查連成幾條線,以決定獎品的好壞。依照老闆的規定,只要以下其中一組格子裡的木板同時倒下,則算連成一線:{1,2,3}、{4,5,6}、{7,8,9}、{1,4,7}、{2,5,8}、{3,6,9}。舉例來說,若2、3、5、7、8、9這六個格子中的木板都倒下,則2、5、8連成一線,且7、8、9也連成一線,總共連成兩條線。(請注意,依規則3、5、7不算連成一線。)此外,老闆也會根據丟到的格子號碼,計算"加碼積分",提供額外的獎賞,詳細規則如下:丟到5號得2分,丟到{2、4、6、8}中的任一號碼得5分,丟到{1、3、7、9}中的任一號碼得8分。例如若2、5、8、9這四格被丟中,則加碼積分為20分。請注意,重複丟到的號碼只算一次分數。
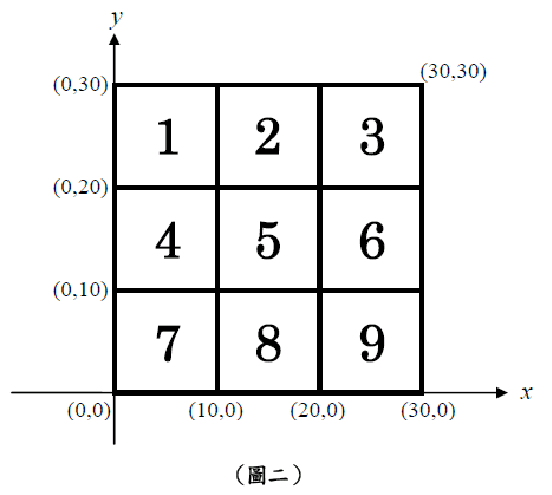
請寫一個程式來模擬玩棒球九宮格的遊戲。為了方便貣見,我們將用二維座標來定義九宮格的位置,如圖二所示。每一格都是相同大小的正方形,7號格左下角的座標為(0,0),3號格右上角座標為(30,30)。在模擬的過程中,會提供每一顆球丟在九宮格上的座標位置。為了簡化問題,若某顆球丟在九宮格上的座標位於某一格內,則判斷打到該格;如果座標位於某一格的邊上,則判斷為打到框架,沒有任何格子被打到。舉例來說,假設一顆球丟到座標位置為(7,13)的地方,由於落在4號格之內,判定打到4號格;假設有另一顆球打在(10,2)(或(10,20))的座標位置,則因為落在框架上,沒有任何格子被打到。當然如果座標落在九宮格外的區域,也沒有任何格子被丟中。

九顆球都丟完之後,夜市的老闆會根據倒下的格子來檢查連成幾條線,以決定獎品的好壞。依照老闆的規定,只要以下其中一組格子裡的木板同時倒下,則算連成一線:{1,2,3}、{4,5,6}、{7,8,9}、{1,4,7}、{2,5,8}、{3,6,9}。舉例來說,若2、3、5、7、8、9這六個格子中的木板都倒下,則2、5、8連成一線,且7、8、9也連成一線,總共連成兩條線。(請注意,依規則3、5、7不算連成一線。)此外,老闆也會根據丟到的格子號碼,計算"加碼積分",提供額外的獎賞,詳細規則如下:丟到5號得2分,丟到{2、4、6、8}中的任一號碼得5分,丟到{1、3、7、9}中的任一號碼得8分。例如若2、5、8、9這四格被丟中,則加碼積分為20分。請注意,重複丟到的號碼只算一次分數。
請寫一個程式來模擬玩棒球九宮格的遊戲。為了方便貣見,我們將用二維座標來定義九宮格的位置,如圖二所示。每一格都是相同大小的正方形,7號格左下角的座標為(0,0),3號格右上角座標為(30,30)。在模擬的過程中,會提供每一顆球丟在九宮格上的座標位置。為了簡化問題,若某顆球丟在九宮格上的座標位於某一格內,則判斷打到該格;如果座標位於某一格的邊上,則判斷為打到框架,沒有任何格子被打到。舉例來說,假設一顆球丟到座標位置為(7,13)的地方,由於落在4號格之內,判定打到4號格;假設有另一顆球打在(10,2)(或(10,20))的座標位置,則因為落在框架上,沒有任何格子被打到。當然如果座標落在九宮格外的區域,也沒有任何格子被丟中。

輸入說明 :
輸入總共有9行。每一行有兩個整數x和y (-20 <= x,y <= 50,x與y由一個空白隔開),代表球的座標。
輸出說明 :
請輸出丟出9顆球之後,根據夜市老闆的規則總共連成幾條線;另外請根據丟到的格子號碼,算出加碼積分。
範例輸入 :
輸入範例1:
7 13
10 2
5 8
-9 19
11 35
3 23
18 0
0 18
40 22
輸入範例2:
12 22
15 11
3 20
3 22
33 27
28 28
16 5
22 -5
35 35
範例輸出 :
輸出範例1:
1 21
輸出範例2:
2 28
遊園接駁車
內容 :
某一遊樂園分為水上樂園與探索樂園,旅客玩完水上樂園之後,接著便排隊搭乘單人客車進入探索樂園遊園。每部車只可搭載一名旅客進入探索樂園,旅客先到先搭車;如果某單人客車已經準備好要搭載旅客,但是此時並沒有等待中的旅客,那麼該輛車就必須等待。若旅客等待客車的時間超過 30 分鐘(包含30分鐘)就會放棄搭乘而離開園區。現在有一個由若干個旅客所組成的旅行團同時來到園區,請問在已知下列三個條件
(1) 該旅行團的旅客數量 (10<=m<=60)
(2) 該旅行團的個別旅客待在水上樂園的分鐘數 (1<=t<=60)
(3) 個別旅客環繞探索樂園的分鐘數 (1<=T<=60)
請撰寫程式計算至少需要幾部單人客車,才能滿足該旅行團所有的旅客,不讓旅客等超過30分鐘。 (m,t,T 皆為整數 )請輸出至少需要單人客車的數量 ?
輸入說明 :
第一行為該旅行團人數,接下來每一行都有兩筆數據,第一筆代表個別旅客待在水上樂園的分鐘數,第二筆代表個別旅客環繞探索樂園的分鐘數。(輸入順序未必按照旅客待在水上樂園的分鐘數排列)
輸出說明 :
至少需要單人客車的數量。
範例輸入 :
11
5 30
40 30
35 5
15 10
30 20
10 40
45 5
50 5
5 10
35 5
50 30
5
10 20
20 30
10 45
10 50
15 30
範例輸出 :
2
3
網路設計
內容 :
某一城市欲建立都會網路,以使每一區公所均可連線到其他各區公所(可能直接連線或透過其他的區公所間接連線)。假設任兩個區公所之間的佈線成本為已知;每一條網路線均為雙向傳送。請寫一程式,印出哪些區公所之間需要施工佈線,以找出此城市使用最低成本完成此都會網路之佈線架構。
輸入說明 :
第一列有兩個正整數n及m,其中n代表區公所個數(n<=10),區公所代碼為W1、W2、W3…Wn。m代表有m個可能的佈線連結兩區公所。其後有m列,每一列之資料依序為兩區公所代碼,及連接此兩區公所之佈線成本。各項資料之間以一個空白分隔;佈線成本為一正整數。
輸出說明 :
印出二列。第一列為佈線架構,印出數組資料,每一組資料為兩個區公所代碼,代表此兩個區公所需要施工佈線,每一組資料包含在一對括號之中。第二列為佈線總成本。各項資料之間以一個空白分隔。
範例輸入 :
7 11
W1 W2 1
W1 W4 4
W2 W3 2
W2 W4 6
W2 W5 4
W3 W5 5
W3 W6 6
W4 W5 3
W4 W7 4
W5 W6 8
W6 W7 3
範例輸出 :
(W1 W2) (W1 W4) (W2 W3) (W4 W5) (W4 W7) (W6 W7)
17
笨小猴
內容:
笨小猴的詞彙量很小,所以每次做英語選擇題的時候都很頭疼。 但是他找到了一種方法,經試驗證明,用這種方法去選擇選項的時候選對的機率非常大!
這種方法的具體描述如下:假設maxn是單詞中出現次數最多的字母的出現次數,minn是單詞中出現次數最少的字母的出現次數,如果maxn-minn是一個質數,那麼笨小猴就認為這是個Lucky Word,這樣的單詞很可能就是正確的答案。
輸入說明:
輸入只有一行,是一個單詞,其中只可能出現小寫字母,並且長度小於100。
輸出說明:
輸出共兩行,第一行是一個字符串,假設輸入的的單詞是Lucky Word,那麼輸出“Lucky Word”,否則輸出“No Answer”;
第二行是一個整數,如果輸入單詞是Lucky Word,輸出maxn-minn的值,否則輸出0。
範例輸入:
範例1: error範例2: olymipic 範例輸出:
範例1: Lucky Word 2範例2: No Answer 0提示:
單詞error中出現最多的字母r出現了3次,出現次數最少的字母出現了1次,3-1=2,2是質數。
單詞olymipic中出現最多的字母i出現了2次,出現次數最少的字母出現了1次,2-1=1,1不是質數。
訂閱:
意見 (Atom)